Historically, studies have suggested that bed thickness distributions tend to have limited dependence on depositional environment and their variability in terms of both distribution type and parameterisation is somewhat limited. Kolmorogov in 1951 used truncated Gaussians to model bed thickness distributions but obtained poor results. Lognormal distributions (McBride, 1962, Enos, 1969) and subsequently exponential distributions (Drummond and Wilkinson 1996) both provided a better fit. Malinverno in 1997 investigated turbidite bed thickness distribution and showed that a fitted straight line on a log-log plot implies a power-law relationship. This relationship suggests that the Earth layering is fractal.
If the Gamma Ray log is transformed to frequency it shows the same power-law relationship, therefore it is a fractal curve meaning that the Geology is typically fractal or scale invariant.
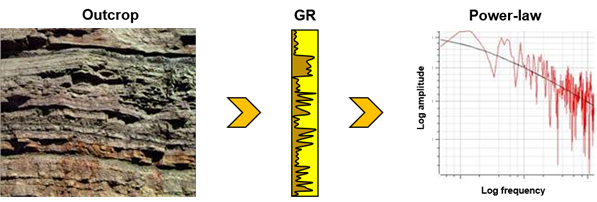
Without a scale it is difficult to discern the size of the outcrop in the picture of bed thickness distribution (left) implying the layering is fractal. Using the GR log (middle) as an input the Earth shows a distinctive power-law distribution (right).
Various studies have claimed good fits for lognormal, exponential and power-law distributions but most of them were based on a fairly limited amount of data until 2014, when Grimston and Connolly analysed bed thickness distributions from a large number of wells from the Caspian Sea to determine the best fit distribution type and the range of parameter values. Their results tend to confirm the findings of earlier studies:
Lognormal distribution tends to best fit the data however other long-tailed distributions, exponential and power-law, fit the data almost as well or in some cases better.
The parameterisation of these distributions tends to be stable.
It is difficult to distinguish between different models for describing bed thickness distributions.
Different depositional environments can give rise to very similar statistical patterns making it difficult to draw unequivocal conclusions from their measurements.
So thanks to the more or less stationary nature of bed thickness distributions that a simple global parameterisation strategy for geophysical processes such as coloured inversion can be so effective.