Let us first consider the basis of Seismic Inversion. Acoustic Impedance is the product of interval velocity and density and is normally represented by the equation:
AI(j) = Vp(j) * p(j)
where Vp is p-wave velocity
and p is density
Seismic reflections are given by the change in the Acoustic Impedance of the layers and are represented by the equation
RC(j) = ( AI(j +1) - AI(j) ) / ( AI(j + 1) + AI(j) )
Now the normal assumption is that the seismic trace is considered to be a primary only reflectivity model convolved with the seismic wavelet which is summed with some uncorrelated noise and can be represented by the equation:
S(t) = R(t) * W(t) + N(t)
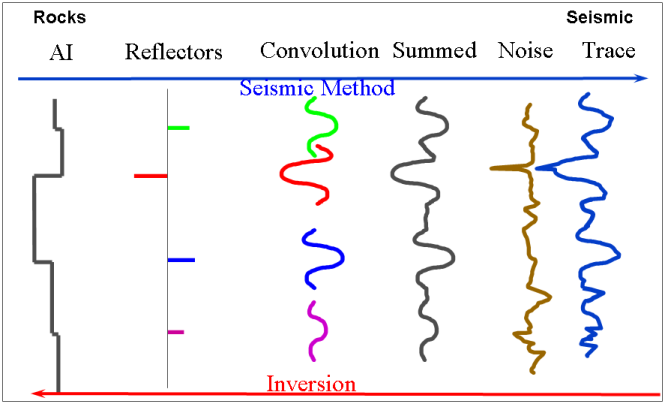
The figure above is a pictorial representation of the convolutional model. So, in simplistic terms the process of moving rocks on the left to seismic on the right is termed the seismic method. On the left we have rock property Acoustic Impedance (AI). So, moving left to right changes in AI at layer boundaries result in normal incident reflection coefficients. Everywhere there is a reflection coefficient it is replaced by a wavelet which is centred and weighted by the reflection coefficient. These individual wavelets are summed and uncorrelated noise is added to generate the seismic trace.
The process of seismic inversion takes us in the opposite direction trying to determine the Acoustic Impedance of the individual rock layers.